Exercise 5 | Regularized Linear Regression and Bias-Variance
=========== Part 1: Loading and Visualizing Data =============
from ex5 import *
from scipy import io as sio
# Load Training Data
print('Loading and Visualizing Data ...')
# Load from ex5data1:
# You will have X, y, Xval, yval, Xtest, ytest in your environment
data = sio.loadmat ('ex5data1.mat')
X = data['X'].reshape(-1)
y = data['y'].reshape(-1)
Xval = data['Xval'].reshape(-1)
yval = data['yval'].reshape(-1)
Xtest = data['Xtest'].reshape(-1)
ytest = data['ytest'].reshape(-1)
# m = Number of examples
m = X.shape[0]
# Plot training data
%matplotlib inline
plt.plot(X, y, 'rx', markersize=10, markeredgewidth=1.5)
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.show()
Loading and Visualizing Data ...

========= Part 2: Regularized Linear Regression Cost ===========
theta = np.array([1, 1])
J, _ = linearRegCostFunction(np.column_stack([np.ones(m), X]), y, theta, 1)
print(f'Cost at theta = [1 ; 1]: {J:f} '
'\n(this value should be about 303.993192)')
Cost at theta = [1 ; 1]: 303.993192
(this value should be about 303.993192)
======= Part 3: Regularized Linear Regression Gradient =========
theta = np.array([1, 1])
J, grad = linearRegCostFunction(np.column_stack([np.ones(m), X]), y, theta, 1)
print(f'Gradient at theta = [1 ; 1]: [{grad[0]:f}; {grad[1]:f}] '
'\n(this value should be about [-15.303016; 598.250744])')
Gradient at theta = [1 ; 1]: [-15.303016; 598.250744]
(this value should be about [-15.303016; 598.250744])
=========== Part 4: Train Linear Regression =============
# Train linear regression with lambda = 0
lambda_ = 0;
theta = trainLinearReg(np.column_stack([np.ones(m), X]), y, lambda_)
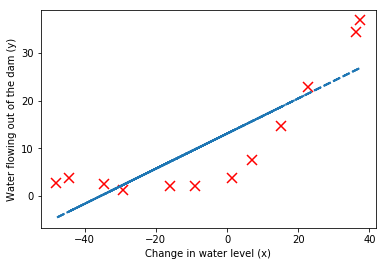
# Plot fit over the data
plt.plot(X, y, 'rx', markersize=10, markeredgewidth=1.5)
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.plot(X, np.matmul(np.column_stack([np.ones(m), X]), theta), '--', linewidth=2)
plt.show()
Optimization terminated successfully.
Current function value: 22.373906
Iterations: 2
Function evaluations: 5
Gradient evaluations: 5
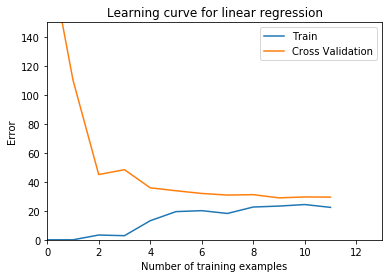
======== Part 5: Learning Curve for Linear Regression ==========
lambda_ = 0
error_train, error_val = learningCurve(np.column_stack([np.ones(m), X]), y,
np.column_stack([np.ones_like(Xval), Xval]), yval, lambda_)
plt.plot(np.arange(m), error_train)
plt.plot(np.arange(m), error_val)
plt.title('Learning curve for linear regression')
plt.legend(['Train', 'Cross Validation'])
plt.xlabel('Number of training examples')
plt.ylabel('Error')
plt.axis([0, 13, 0, 150])
print('# Training Examples\tTrain Error\tCross Validation Error')
for i in range(m):
print(f' \t{i}\t\t{error_train[i]:f}\t{error_val[i]:f}')
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 1
Function evaluations: 3
Gradient evaluations: 3
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 2
Function evaluations: 6
Gradient evaluations: 6
Optimization terminated successfully.
Current function value: 3.286595
Iterations: 9
Function evaluations: 15
Gradient evaluations: 15
Optimization terminated successfully.
Current function value: 2.842678
Iterations: 8
Function evaluations: 14
Gradient evaluations: 14
Optimization terminated successfully.
Current function value: 13.154049
Iterations: 22
Function evaluations: 34
Gradient evaluations: 34
Optimization terminated successfully.
Current function value: 19.443963
Iterations: 22
Function evaluations: 34
Gradient evaluations: 34
Optimization terminated successfully.
Current function value: 20.098522
Iterations: 18
Function evaluations: 28
Gradient evaluations: 28
Optimization terminated successfully.
Current function value: 18.172859
Iterations: 2
Function evaluations: 5
Gradient evaluations: 5
Optimization terminated successfully.
Current function value: 22.609405
Iterations: 2
Function evaluations: 5
Gradient evaluations: 5
Optimization terminated successfully.
Current function value: 23.261462
Iterations: 2
Function evaluations: 5
Gradient evaluations: 5
Optimization terminated successfully.
Current function value: 24.317250
Iterations: 2
Function evaluations: 5
Gradient evaluations: 5
Optimization terminated successfully.
Current function value: 22.373906
Iterations: 2
Function evaluations: 5
Gradient evaluations: 5
# Training Examples Train Error Cross Validation Error
0 0.000000 205.121096
1 0.000000 110.300366
2 3.286595 45.010232
3 2.842678 48.368911
4 13.154049 35.865141
5 19.443963 33.829957
6 20.098522 31.970987
7 18.172859 30.862446
8 22.609405 31.135998
9 23.261462 28.936207
10 24.317250 29.551432
11 22.373906 29.433818
===== Part 6: Feature Mapping for Polynomial Regression =======
p = 8
# Map X onto Polynomial Features and Normalize
X_poly = polyFeatures(X, p)
X_poly, mu, sigma = featureNormalize(X_poly) # Normalize
X_poly = np.insert(X_poly, 0, 1, axis=1) # Add Ones
# Map X_poly_test and normalize (using mu and sigma)
X_poly_test = polyFeatures(Xtest, p)
X_poly_test = X_poly_test - mu
X_poly_test = X_poly_test / sigma
X_poly_test = np.insert(X_poly_test, 0, 1, axis=1) # Add Ones
# Map X_poly_val and normalize (using mu and sigma)
X_poly_val = polyFeatures(Xval, p)
X_poly_val = X_poly_val - mu
X_poly_val = X_poly_val / sigma
X_poly_val = np.insert(X_poly_val, 0, 1, axis=1) # Add Ones
print('Normalized Training Example 1:')
print(f' {X_poly[0, :]} ')
Normalized Training Example 1:
[ 1. -0.378244 -0.788662 0.190329 -0.737591 0.320252 -0.617152
0.359835 -0.531091]
====== Part 7: Learning Curve for Polynomial Regression ========
lambda_ = 0;
theta = trainLinearReg(X_poly, y, lambda_)
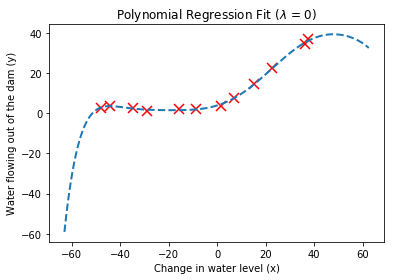
# Plot training data and fit
plt.figure()
plt.plot(X, y, 'rx', markersize=10, markeredgewidth=1.5)
plotFit(min(X), max(X), mu, sigma, theta, p);
plt.xlabel('Change in water level (x)')
plt.ylabel('Water flowing out of the dam (y)')
plt.title(f'Polynomial Regression Fit ($\lambda$ = {lambda_:g})')
plt.show()
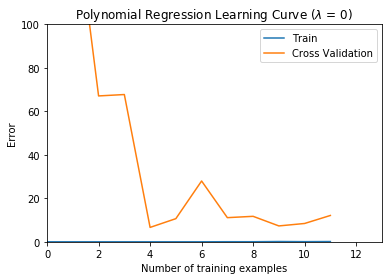
plt.figure()
error_train, error_val = learningCurve(X_poly, y, X_poly_val, yval, lambda_)
plt.plot(np.arange(m), error_train)
plt.plot(np.arange(m), error_val)
plt.title(f'Polynomial Regression Learning Curve ($\lambda$ = {lambda_:g})')
plt.xlabel('Number of training examples')
plt.ylabel('Error')
plt.axis([0, 13, 0, 100])
plt.legend(['Train', 'Cross Validation'])
print(f'Polynomial Regression (lambda = {lambda_:g})\n')
print('# Training Examples\tTrain Error\tCross Validation Error')
for i in range(m):
print(f' \t{i}\t\t{error_train[i]:f}\t{error_val[i]:f}')
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.119425
Iterations: 200
Function evaluations: 372
Gradient evaluations: 372
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 2
Function evaluations: 4
Gradient evaluations: 4
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 6
Function evaluations: 9
Gradient evaluations: 9
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 15
Function evaluations: 27
Gradient evaluations: 27
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 4
Function evaluations: 13
Gradient evaluations: 13
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 17
Function evaluations: 35
Gradient evaluations: 35
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 37
Function evaluations: 72
Gradient evaluations: 72
Optimization terminated successfully.
Current function value: 0.000000
Iterations: 147
Function evaluations: 274
Gradient evaluations: 274
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.040218
Iterations: 200
Function evaluations: 380
Gradient evaluations: 380
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.035614
Iterations: 200
Function evaluations: 366
Gradient evaluations: 366
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.131620
Iterations: 200
Function evaluations: 371
Gradient evaluations: 371
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.068496
Iterations: 200
Function evaluations: 350
Gradient evaluations: 350
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.119425
Iterations: 200
Function evaluations: 372
Gradient evaluations: 372
Polynomial Regression (lambda = 0)
# Training Examples Train Error Cross Validation Error
0 0.000000 161.442168
1 0.000000 160.792292
2 0.000000 67.084922
3 0.000000 67.726849
4 0.000000 6.616987
5 0.000000 10.643050
6 0.000000 27.963489
7 0.040218 11.105429
8 0.035614 11.714711
9 0.131620 7.300176
10 0.068496 8.426525
11 0.119425 12.112653
=========== Part 8: Validation for Selecting \(\lambda\) =============
lambda_vec, error_train, error_val = validationCurve(X_poly, y, X_poly_val, yval)
plt.plot(lambda_vec, error_train)
plt.plot(lambda_vec, error_val)
plt.legend(['Train', 'Cross Validation'])
plt.xlabel('$\lambda$')
plt.ylabel('Error')
print('lambda\t\tTrain Error\tValidation Error')
for i in range(len(lambda_vec)):
print(f' {lambda_vec[i]:f}\t{error_train[i]:f}\t{error_val[i]:f}')
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.119425
Iterations: 200
Function evaluations: 372
Gradient evaluations: 372
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.180723
Iterations: 200
Function evaluations: 370
Gradient evaluations: 370
Optimization terminated successfully.
Current function value: 0.243172
Iterations: 195
Function evaluations: 377
Gradient evaluations: 377
Warning: Maximum number of iterations has been exceeded.
Current function value: 0.371283
Iterations: 200
Function evaluations: 377
Gradient evaluations: 377
Optimization terminated successfully.
Current function value: 0.636703
Iterations: 118
Function evaluations: 218
Gradient evaluations: 218
Optimization terminated successfully.
Current function value: 1.360572
Iterations: 78
Function evaluations: 146
Gradient evaluations: 146
Optimization terminated successfully.
Current function value: 2.917649
Iterations: 61
Function evaluations: 101
Gradient evaluations: 101
Optimization terminated successfully.
Current function value: 6.830463
Iterations: 34
Function evaluations: 62
Gradient evaluations: 62
Optimization terminated successfully.
Current function value: 14.937646
Iterations: 13
Function evaluations: 24
Gradient evaluations: 24
Optimization terminated successfully.
Current function value: 31.878154
Iterations: 15
Function evaluations: 25
Gradient evaluations: 25
lambda Train Error Validation Error
0.000000 0.119425 12.112653
0.001000 0.146681 15.167242
0.003000 0.166711 15.938570
0.010000 0.218028 17.154297
0.030000 0.275169 13.215280
0.100000 0.438662 7.926893
0.300000 0.868160 4.760834
1.000000 1.958695 4.263359
3.000000 4.525105 3.832176
10.000000 14.825808 8.889725
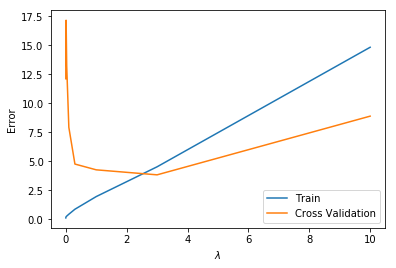
Computing test set error
可以看到,当\(\lambda = 3\)时验证集误差最小
lambda_ = 3
theta = trainLinearReg(X_poly, y, lambda_)
error_test = linearRegCostFunction(X_poly_test, ytest, theta, 0)[0]
print(f'Error at lambda = 3: {error_test:f} '
'\n(this value should be about 3.8599)')
Optimization terminated successfully.
Current function value: 14.937646
Iterations: 13
Function evaluations: 24
Gradient evaluations: 24
Error at lambda = 3: 3.572027
(this value should be about 3.8599)
Plotting learning curves with randomly selected examples
比较复杂,关掉迭代过程显示,重新写一遍
lambda_ = 0.01
repeat = 50
m = X_poly.shape[0]
error_train = np.zeros(m)
error_val = np.zeros(m)
for i in range(m):
# Initialize Theta
initial_theta = np.zeros(X_poly.shape[1])
# Create "short hand" for the cost function to be minimized
costFunction = lambda t, X, y: linearRegCostFunction(X, y, t, lambda_)[0]
gradFunction = lambda t, X, y: linearRegCostFunction(X, y, t, lambda_)[1]
# Now, costFunction is a function that takes in only one argument
options = {'maxiter': 200, 'disp': False}
error_train_temp = 0
error_val_temp = 0
for j in range(repeat):
random_i = np.random.permutation(m)[:i + 1]
# Minimize using fmincg
res = opt.minimize(costFunction, initial_theta, args=(X_poly[random_i], y[random_i]), method='CG', jac=gradFunction, options=options)
theta = res.x
error_train_temp += linearRegCostFunction(X_poly[random_i], y[random_i], theta, 0)[0]
error_val_temp += linearRegCostFunction(X_poly_val[random_i], yval[random_i], theta, 0)[0]
error_train[i] = error_train_temp / repeat
error_val[i] = error_val_temp / repeat
plt.plot(np.arange(m), error_train)
plt.plot(np.arange(m), error_val)
plt.title(f'Polynomial Regression Learning Curve ($\lambda$ = {lambda_:g})')
plt.xlabel('Number of training examples')
plt.ylabel('Error')
plt.axis([0, 13, 0, 100])
plt.legend(['Train', 'Cross Validation'])
plt.show()
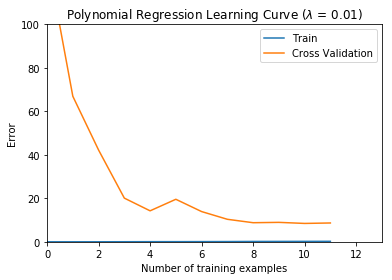
用了随机采样平均值之后曲线平滑了不少。

